Discover a comprehensive collection of UPSC Prelims Topic Wise Questions focusing on Basic Numeracy, specifically covering Permutation, Combination, and Probability. Dive into a diverse array of questions designed to enhance your understanding and preparation for the UPSC Preliminary examination in these fundamental mathematical concepts. This resource offers a structured approach to mastering key principles and techniques necessary for success in permutation, combination, and probability problems. Whether you’re a beginner or an advanced candidate, these meticulously crafted questions provide valuable insights and practice opportunities to excel in the competitive UPSC environment. With a strategic emphasis on topic-wise questions, aspirants can refine their problem-solving skills and develop a deeper comprehension of these mathematical concepts. Elevate your preparation, grasp essential insights, and boost your confidence to ace the UPSC Prelims with proficiency in permutation, combination, and probability within the realm of basic numeracy.
Q1. A table has three drawers. It is known that one of the drawers contains two silver coins, another contains two gold coins and the third one contains a silver coin and gold coin. One of the drawers is opened at random and a coin is drawn. It is found to be a silver coin. What is the probability that the other coin in the drawer is a gold coin? (1995)
(a) 0.25
(b) 1.00
(c) 0.33
(d) 0.60
Ans. (c)
| Drawer 1 | Drawers 2 | Drawer 3 |
| 2 silver coins | 2 gold coins | 1 silver coin + 1 gold coin |
If one drawing one silver coin, one gold coin is left, it means that, the drawer is 3
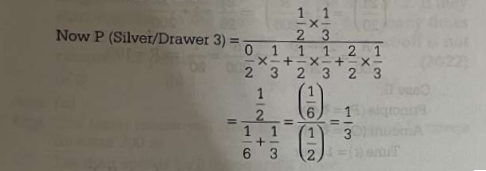
Q2. A student has 60% chance of passing in English and 54% chance of passing in both English and Mathematics. What is the percentage probability that he will fail in Mathematics? (1995)
(a) 12
(b) 36
(c) 4
(d) 10
Ans. (d)
Probability of passing in English
= P(E)= 60/100 = 0.6
Probability of passing in both Maths and English
= P(E ∩ M) = 54/100 = 0.54
Probability of passing in Maths = P(M)
P(M) and P(E), both are independent events.
P(E ∩ M) = P(E) X P(M)
P(M) = P(E ∩ M)/P(E) = 0.54/0.6 = 0.9
… Probability of failing in Maths=1-0.9 = 0.1 = 10%
Hence, the percentage probability that he will fail in Mathematics = 0.1×100=10%
Q3. Two packs of cards are thoroughly mixed and shuffled and two cards are drawn at random, one after the other. What is the probability that both of them are jacks? (1995)
(a) 1/13
(b) 2/13
(c) 7/1339
(d) 1/169
Ans. (c)
Total number of cards = 2 x 52 = 104
and total number of jacks = 2 x 4 = 8
Probability for the jack in first draw = 8/104
and probability for the jack in second draw = 7/103
Both the events are independent events.
Required probability = (8/104) x (7/103) = 7/1339
Q4. When three coins are tossed together, the probability that all coins have the same face up, is (1997)
(a) 1/3
(b) 1/6
(c) 1/4
(d) 1/12
Ans. (c)
When three coins are tossed simultaneously then, total outcomes = 8 [HHH, HHT, HTH, HTT, TΗΗ, ΤΗΤ, TTH, TTT] Favourable outcome = 2 [HHH, TTT]
P (Same face up) = 2/8 = 1/4
Q5. In a factory quality assurance test is conducted on various samples for a specific characteristic value of the product. The values and the number of samples are as given in the following table. (1999)
| Characteristic value, X | Number of samples |
| 10 | 3 |
| 11 | 7 |
| 12 | 10 |
| 13 | 15 |
| 14 | 28 |
| 15 | 33 |
| 16 | 24 |
| 17 | 11 |
| 18 | 10 |
| 19 | 6 |
| 20 | 3 |
Consider the following statements based on the table
I. The probability that X ≤ 15 is 0.64.
II. The probability that 13 < X ≤ 17 is greater than 0.64.
III. The probability that X = 15 is less than 0.22.
Which of the above statement is/are not true?
(a) I alone
(b) I and II
(c) II and III
(d) I, II and III
Ans. (c)
Total number of samples
=3+7+10+15+28+33+24+11+10+6+3 = 150
Probability (P) = Number of samples of (X) / Total number of samples (150)
Now, we consider the given statements
In case you still have your doubts, contact us on 9811333901.
For UPSC Prelims Resources, Click here
For Daily Updates and Study Material:
Join our Telegram Channel – Edukemy for IAS
- 1. Learn through Videos – here
- 2. Be Exam Ready by Practicing Daily MCQs – here
- 3. Daily Newsletter – Get all your Current Affairs Covered – here
- 4. Mains Answer Writing Practice – here
